7.2 Модель системной динамики города
7.2.1 Назначение модели
Математическая модель расчета интегрального (системно-динамического) прогноза демографических, экономических показателей СЭР (далее – Модель) предназначена для:
– Определения долгосрочных трендов (регрессионной, аппроксимирующей функции) изменения базовых показателей СЭР города;
– Формирования динамического прогноза (на основе динамической функции) базовых показателей СЭР, ограниченных коридором значений долгосрочных трендов;
– Расчета корреляционных функций, описывающих меру взаимного влияния показателей друг на друга и восприимчивость к изменению внешних факторов.
Модель преобразует набор фактических, ежегодных (не менее чем за 6 лет) значений по 27 макроэкономическим показателям СЭР города и дополнительным 4 макроэкономическим показателям, характеризующих внешние факторы, в наборы следующих значений для каждого города:
– 27 макроэкономических показателей СЭР города за ретроспективный (до 2000 года) и перспективный (до 2050 года) периоды времени,
– корреляционные матрицы размерности 31 показатель х 31 показатель х 50 годовых периода, отражающих степени взаимного влияния изменения показателей СЭР.
7.2.2 Базовый вид модели
Под базовым видом модели будем понимать уравнения модели (целевой функции) в общем виде.
Базовым дифференциальным уравнением Модели является уравнение затухающих колебаний, описывающее изменение показателей системы \(x(t)\) во времени, \[\begin{align*} \frac{d^{2} x(t)}{dt^{2}}+ \gamma \frac{dx(t)}{dt} + \omega^{2}x(t)=f(t), (1) \end{align*}\] где параметрами системы являются:
\(\gamma\) - характеристика затухания колебаний системы из-за сопротивления («трения») в системе,
\(\omega\) - собственная частота колебаний системы в отсутствие сопротивления («трения»),
\(f\) – совокупность внешних воздействий.
Зависимости показателей от времени представляются суммой 42-х базовых функций с различными периодами колебаний:
\[\begin{align*}
x(t)=\sum_{i=1}^{21}(C_{i}cos\omega_{i}t+S_{i}sin\omega_{i}t)e^{-a_{i}t} (2)
\end{align*}\]
Для определения коэффициентов \((C, S, \omega, a)\) к динамической функции \(x(t)\) применяется преобразование Лапласа
\[\begin{align*}
L\{x(t)\}(s)=\int_{0}^{\infty}x(t) e^{-st} dt. (3)
\end{align*}\]
Или в явном виде:
\[\begin{align*}
L\{x(t)\}(s)=\sum_{i=1}^{21}(C_{i}\frac{s}{(s+a_{i})^{2}+\omega_{i}^{2}}+S_{i}\frac{\omega_{i}}{(s+a_{i})^{2}+\omega_{i}^{2}}). (3.1)
\end{align*}\]
На основе имеющихся статистических данных рассчитываются параметры \((C, S, \omega, a)\) уравнения (3.1), а затем строится динамическая функция \(x(t)\) (зависимость показателя x от времени) и скорость изменения показателя \(dx(t)/dt\).
Для всех анализируемых показателей СЭР наибольший вклад дают колебания с периодами от 6 до 68 лет.
Функции \(x(t)\), полученные в результате «динамического» анализа, используются для оценки влияния во времени изменения одного показателя (управленческие решения) на другие, в том числе на себя.
Корреляционная функция влияния показателя \(x(t)\) на скорость изменения показателя y вычисляется в виде
\[\begin{align*}
K_{xy}(\tau)=\int_{0}^{\infty}x(t)y`(t+\tau)dt, (4)
\end{align*}\]
где:
\(K_{xy}\) – корреляционная матрица влияния показателя \(x\) на изменение показателя \(у\),
\(y`(t+\tau)\) – скорость изменения показателя СЭР y в момент времени \(t + \tau\), для которого рассчитывается влияние значения \(х(t)\) в момент времени \(t\),
\(\tau\) - период времени с начала действия изменений показателя \(x\).
Исходные данные, а также краевые или граничные условия, для построения динамической функции (2) для показателей отражающих потоки ресурсов (не накопительные показатели: численность населения, общая площадь жилья, баланс бюджета города, накопления граждан), задаются с помощью четырех-параметрических сигмоидальных кривых, которые пригодны не только для аппроксимации в ретроспективном периоде, но и для экстраполяции на прогнозный период показателей (см. Раздел 6).
\[\begin{align*}
X(t)=\frac{A+B(t⁄d)^{c}}{1+(t⁄d)^{c}},(5)
\end{align*}\]
где A, B, c, d – параметры соответствующих соотношений;
A – значение функции при t = 0 (за 0 принято 1 января 1999 года);
B – предельный уровень функции при t = (в «будущем»);
d – дата перегиба функции при t = d;
c – определяет угол наклона кривой в точке перегиба.
7.2.3 Описание входных переменных модели
7.2.3.1 Перечень входных переменных модели
Модель расчета интегрального прогноза демографических и экономических показателей СЭР использует в качестве входных данных ретроспективные значения следующих показателей за период не менее 6-и лет:
| № | Код | Показатель | Ед.изм. |
|---|---|---|---|
| 1 | C013 | Численность населения на 1 января текущего года | человек |
| 2 | C034 | Число родившихся | человек |
| 3 | C035 | Число умерших | человек |
| 4 | C037 | Прибыло населения (миграция) | человек |
| 5 | C038 | Выбыло населения (миграция) | человек |
| 6 | C041 | Население трудоспособного возраста | человек |
| 7 | C096 | Ввод в действие многоквартирных жилых домов | м2 |
| 8 | C149 | Общая площадь жилых помещений | м2 |
| 9 | C221 | Среднесписочная численность работников организаций, всего | человек |
| 10 | C241 | Фонд заработной платы всех работников организаций, всего | рублей |
| 11 | C698 | Налогооблагаемые денежные доходы физических лиц и инд. предпринимателей | рублей |
| 12 | C699 | Доходы населения: социальные и другие выплаты | рублей |
| 13 | C712 | Денежные доходы населения на 1 жителя | руб. в год |
| 14 | C713 | Обязательные платежи и взносы на 1 жителя | руб. в год |
| 15 | C714 | Реальные располагаемые доходы на 1 жителя | руб. в год |
| 16 | C757 | Интегральная обеспеченность ОСЭН по городу | % |
| 17 | C049 | Доходы городского бюджета, всего | млн. руб. |
| 18 | C065 | Расходы городского бюджета, всего | млн. руб. |
| 19 | C087 | Инвестиции в осн. капитал осуществляемые организациями (без мал. бизнеса) | млн. руб. |
| 20 | C706 | Валовый городской продукт (ВГП) | млн. руб. |
| 21 | C708 | Налоговые доходы бюджетов всех уровней | млн. руб. |
| 22 | C709 | Доходы местного бюджета (налоговые) | млн. руб. |
| 23 | C433 | Оборотные активы | млн. руб. |
| 24 | C475 | Выручка (За отчетный период) | млн. руб. |
| 25 | C711 | Себестоимость полная (выручка - чистая прибыль) | млн. руб. |
| 26 | C707 | Валовая добавленная стоимость МСП | млн. руб. |
| 27 | C409 | Основные средства | млн. руб. |
| 28 | C715 | Региональный Индекс Потребительских Цен (ИПЦ) | ед. |
| 29 | C716 | Курс доллара | руб. / $ |
| 30 | C717 | Платежный баланс (сальдо импорта и экспорта) РФ | долларов |
| 31 | C718 | Валовый Внутренний Продукт (ВВП) РФ | млн. руб. |
7.2.3.2 Источники данных
Источником исходных данных для показателей (переменных) является База данных показателей муниципальных образований, размещённая в сети Интернет по адресу - https://rosstat.gov.ru/storage/mediabank/Munst.htm, за исключением следующих случаев:
| № | Наименование показателя (набора) | Источник данных |
|---|---|---|
| 1 | Валовый городской продукт | Математическая модель прогнозирования экономических показателей |
| 2 | Интегральная обеспеченность ОСЭН по городу | Математическая модель оценки качества городской среды |
| 3 | Выручка, Прибыль (убыток) от продаж, Основные средства предприятий | Бухгалтерские балансы |
| 4 | Денежные доходы, обязательные платежи и взносы, реальные располагаемые доходы | Росстат |
| 5 | Региональный ИПЦ | Росстат |
| 6 | Курс доллара, Платежный баланс (сальдо импорта и экспорта) РФ, ВВП РФ, Ставка ЦБ | Центральный банк РФ |
7.2.4 Описание результата модели
7.2.4.1 Перечень выходных данных модели
Модель расчета интегрального прогноза демографических и экономических показателей СЭР формирует в качестве выходных данных значения показателей описанных в Перечне входных переменных модели на ретроспективный (до 2000 года) и перспективный (до 2050 года) периоды, а так же матрицу чувствительности значений показателей к изменению каждого показателя на годовые периоды времени (корреляционная матрица).
7.2.5 Калибруемые параметры модели
Для каждого показателя из Перечня входных переменных модели рассчитываются следующие калибруемые параметры модели:
\(\gamma\) - характеристика затухания колебаний системы (Пример на Рисунке 1),
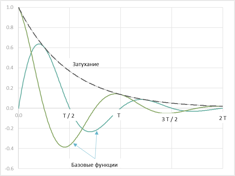
\(\omega\) - собственная частота колебания системы в отсутствие сопротивления среды, приведенная на Рисунке 2.
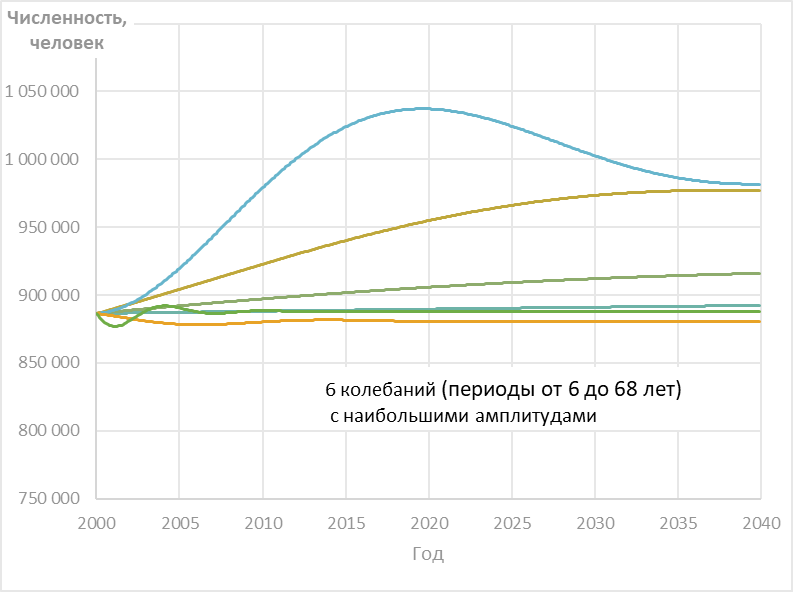
\(C, S, \omega , a\) – постоянные параметры интегрирования, рассчитываемые на исходных данных для 21 частоты, определяемые по начальным (фактические значения показателей) и краевым условиям (доверительного интервала аппроксимирующей показатель функции).
7.2.6 Калибровка модели
7.2.6.1 Характеристики и объем массива данных для разработки модели
Исходный объем массива данных для каждого города составляет не менее 186 значений или 6 годовых значений по каждому из 31 показателя социально-экономического развития.
Фактические ретроспективные данные по группе показателей, связанных между собой:
– численность населения, рождаемость, смертность, количество прибывших, количество убывших;
– доходы населения, удельные доходы на одного жителя, численность, региональный ИПЦ;
– расходы городского бюджета, удельные расходы на одного жителя, численность, региональный ИПЦ;
– валовый городской продукт (ВГП), удельный ВГП на одного человека трудоспособного возраста, население трудоспособного возраста, среднесписочная численность работников, региональный ИПЦ.
Для каждого показателя из Перечня входных переменных модели производится расчет параметров нелинейных аппроксимирующих функций, ограничивающих область допустимых значений динамической функции, по следующему порядку:
– аппроксимирующие функции выбираются в форме сигмоид, что позволяет проводить экстраполяцию (прогноз) на перспективный период;
– параметры аппроксимирующих функций рассчитываются так, чтобы минимизировать ошибку по всем показателям одновременно;
– оценка погрешности аппроксимации;
– построение полосы возможного рассеяния на перспективный период;
– в приведенных примерах на Рисунке 3 полосы рассеяния показаны штриховыми линиями для достоверности 90 %;
– расчет области допустимых значений показателей и темпов их изменения производится с помощью вычисления аппроксимирующей функции (5) (Рисунок 3).
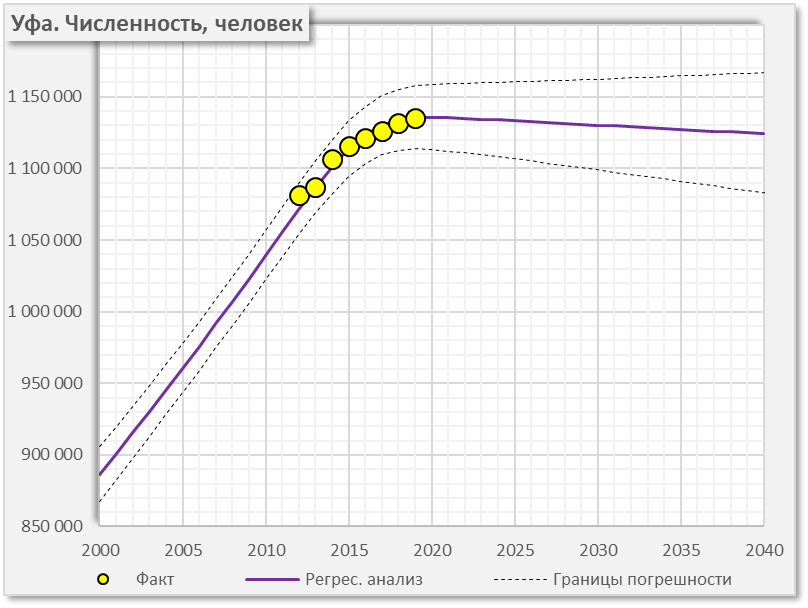
7.2.6.2 Показатели точности калибровки модели
Для каждого показателя, приведенного в Перечне входных переменных модели, рассчитываются следующие показатели точности исходя из принятого за постоянную величину доверительного интервала в 90%:
\(P\) – доверительная вероятность (по умолчанию принята за 90%)
\(\varepsilon\) – абсолютная ошибка (см. пример на рисунке 4)
\(err(t)\) - относительная ошибка, %
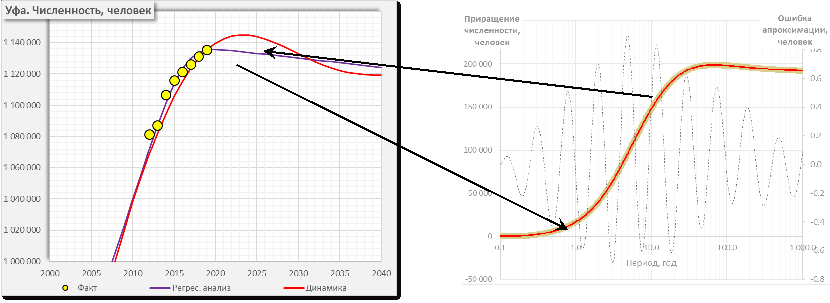
7.2.7 Результат применения модели
По результатам опытной эксплуатации математической модели на 44 городах были получены следующие усредненные отклонения фактических значений показателей от значений, полученных с использованием динамической модели.
Максимальный размер отклонений, зафиксирован по показателям, имеющим рукотворную природу «Обязательные платежи и взносы на 1 жителя», «Инвестиции в основной капитал» или высокую волатильность «Оборотные активы организаций».
| Наименование показателя | Интегральная ошибка динамической модели, % |
|---|---|
| Численность населения на 1 января текущего года | 0,12% |
| Число родившихся | 0,20% |
| Число умерших | 0,33% |
| Прибыло населения (миграция) | 1,12% |
| Выбыло населения (миграция) | 1,25% |
| Население моложе трудоспособного возраста | 0,37% |
| Население трудоспособного возраста | 1,10% |
| Население старше трудоспособного возраста | 0,16% |
| Доходы городского бюджета, всего | 0,70% |
| Расходы городского бюджета, всего | 0,57% |
| Инвестиции в осн. капитал осуществляемые организациями (без мал. бизнеса) | 5,07% |
| Введено в действие жилых домов на территории муниципального образования | 2,71% |
| Общая площадь жилых помещений | 0,85% |
| Среднесписочная численность работников организаций, всего | 0,99% |
| Фонд заработной платы всех работников организаций, всего | 2,57% |
| Основные средства организаций | 2,13% |
| Оборотные активы организаций | 2,54% |
| Выручка организаций | 2,28% |
| Налогооблагаемые денежные доходы физических лиц и инд. предпринимателей | 2,78% |
| Доходы населения: социальные и другие выплаты | 3,18% |
| Валовый городской продукт (ВГП) | 2,27% |
| Валовая добавленная стоимость малого и среднего предпринимательства (МСП) | 4,25% |
| Налоговые доходы бюджетов всех уровней | 3,75% |
| Доходы местного бюджета (налоговые) | 0,56% |
| Полная себестоимость | 2,56% |
| Денежные доходы населения на 1 жителя | 3,99% |
| Обязательные платежи и взносы на 1 жителя | 6,35% |
| Реальные располагаемые доходы на 1 жителя | 3,71% |
| Интегральная обеспеченность ОСЭН по городу | 0,14% |
| Максимальное значение | 6,4% |
| Медианное значение | 2,1% |
| Минимальное значение | 0,1% |
Использование предложенной модели при оценке принятия решений необходимо вести, с учетом достигнутых уровней ошибки.
Размер ошибок имеет склонность к снижению в ходе увеличения объема исходных статистических данных.
7.2.8 Требования к поддержке модели и регулярности ее рекалибровки.
Поддержка модели заключается в ежегодном добавлении или уточнении фактических значений по исходным показателям для расчета, приведенным в Перечне входных переменных модели. Рекалибровка модели происходит в автоматическом режиме, по факту загрузки новых значений показателей по городам.
7.2.9 Допущения, необходимые для проведения расчетов
Ключевыми допущениями, принимаемыми при проведении расчетов, являются:
– наличие фактических значений по всем показателям для города, указанным в Перечне входных переменных модели,
– наличие фактических значений минимум за 6 лет,
– группы показателей по демографии, экономике и качеству городской среды являются условно-независимыми (ортогональными),
– данные муниципальной статистики (Росстат) обладают преимуществом (большей точностью) при формировании исходных показателей переменных.
7.2.10 Полное описание алгоритма проведения расчетов
Алгоритм проведения расчетов состоит из следующих шагов:
Подготовка исходных данных включающих фактические значения входных переменных модели, указанных в Перечне входных переменных модели.
Определение начальных параметров регрессионной модели A, B, c, d методом наименьших квадратов, минимизирующих ошибку по всем показателям одновременно для каждого города и каждой группы социально-экономических показателей города:
- Демографических (численность населения, количество родившихся и умерших, прибыло и выбыло населения, численность населения трудоспособного возраста)
- Экономических (среднесписочная численность работников организаций, фонд заработной платы всех работников организаций, выручка и прибыль организаций, доходы МСП, основные и оборотные активы, инвестиции в основной капитал)
- Городских (Валовый городской продукт, доходы и расходы бюджета, доходы и расходы населения, Налоговые доходы бюджетов всех уровней)
- Социальных (общая площадь жилых помещений, ввод в действие многоквартирных жилых домов, введено в действие жилых домов, обеспеченность ОСЭН по городу)
Вычисление прогнозных и восстановление отсутствующих ретроспективных показателей социально-экономического развития на основе регрессионной модели.
Определение ошибок расчета
\[\begin{align*}
\varepsilon_{[20XX]} = x(20XX)-X_{[20XX]}, (6)
\end{align*}\]
где:
\(\varepsilon_{[20XX]}\) – величина ошибки по каждому показателю на 20XX год
\(x(20ХХ)\) – значение показателя полученное на основе регрессионной модели п.3
\(X_{[20ХХ]}\) - фактическое значение показателя
- Уточнение параметров A, B, c, d методом Ньютона безусловной оптимизации суммы квадратов погрешностей \(\sum\varepsilon^{2}\) , полученныхв п. 4
- Итерационное повторение шагов 2, 3, 4, 5 до достижения возможного минимума суммы квадратов погрешностей
- Построение верхней и нижней границ прогноза регрессионной модели. Ошибка аппроксимации \(err(t)\) включают две составляющие: постоянную \(\varepsilon_{const}\) и переменную \(\varepsilon_{var}(t-t_{0})\), равную 0 в начальной точке \(t_{0}\) (в представленных результатах \(t_{0}\) соответствует 1 января 2019 года)
\[\begin{align*} err(t)^{2}=\varepsilon_{const}^{2} + \varepsilon_{var}^{2}(t-t_{0}). (7) \end{align*}\]
- Для построения верхней \(H(t)\) и нижней \(L(t)\) границ значений показателей регрессионной модели ошибка \(err(t)\) умножается на квантиль \(z_{[P]}\), зависящий от доверительной вероятности \(P\), количества параметров и количества фактических значений (для приведенного примера при \(P=90\%\), 16-и параметрах и 90 фактических значений \(z_{[90\%]} = 1.673\)):
\[\begin{align*} H(t)=X(t)e^{z_{[P]}err(t)}, (8) L(t)=X(t)e^{-z_{[P]}err(t)}. (9) \end{align*}\]
- Определение параметров динамической функции \((C, S, \omega, a)\) на основе имеющихся статистических данных, верхней и нижней границ значений показателей регрессионной модели на основании уравнения (2).
- Формирование модельных значений для каждого показателя на прогнозный и ретроспективный периоды на основе динамической функции, построенной с использование параметров \((C, S, \omega, a)\).
- Расчет корреляционных матриц для каждого показателя по формуле (4) исходя из полученных модельных значений.
7.2.11 Область (границы) допустимого применения математических моделей
Областью (границей) допустимого применения математических моделей является:
– формирование инерционного среднесрочного и долгосрочного прогноза основных показателей социально-экономического развития городов,
– восстановление отсутствующих значений по показателям социально-экономического развития городов на ретроспективном периоде не ранее 2000 года,
– создание корреляционных матриц для реализации моделей оценки влияния параметров инвестиционного проекта на социально-экономическое развитие городов на среднесрочном (1-5 лет) и долгосрочном (5-15 лет) горизонтах времени.
