7.1 Модель прогнозирования численности населения
7.1.1 Назначение
Математическая модель демографических показателей СЭР (далее – Модель) предназначена для расчета прогноза значений демографических показателей (население, рождаемость, смертность, миграция) социально-экономического развития населенных пунктов (городов, регионов, стран).
Набор демографических показателей входит в состав концепции и методики оценки влияния инвестиционных проектов на социально-экономическое развитие. Зеленой рамкой на рисунке выделено место рассчитываемых показателей в общей структуре показателей СЭР.
Демографические показатели СЭР являются базовыми показателями, характеризующими состояние и развитие города, являются исходными для расчета показатели социального (обеспеченность объектами социально-экономического назначения, реальные располагаемые доходы населения) и экономического развития (объемы потребления, фондов оплаты труда и местных налогов). Логические связи демографических показателей, включенных в Модель с другими базовыми показателями, СЭР представлены на рисунке.
Модель позволяет на основе неполного ряда ретроспективных значений показателей сформировать, как прогнозные значения на долгосрочный (десятки лет) и среднесрочный (годы) период времени, так и восстановить отсутствующие, откорректировать «аномальные» значения на ретроспективном периоде времени.
Основные задачи демографической модели:
1. Определение устойчивых коэффициентов тренда, описывающего изменения значений показателей во времени
2. Восстановление ретроспективных значений показателей, с помощью интерполяции для повышения качества муниципальной статистики
3. Расчет базового (инерционного) прогноза демографических показателей на расчетный период
4. Расчет сценарного демографических показателей, с учетом возможных «рукотворных» событий (инвестиционный проект, расширение территорий, катастрофические явления), происходящих одномоментно («скачок») изменяющим или не изменяющим тренд по выбору пользователя Модели
7.1.2 Основные параметры, показатели и обозначения
Модель позволяет производить прогнозные расчеты для следующих демографических показателей:
| № | Наименование демографического показателя | Ед. изм. |
|---|---|---|
| 1 | Численность | человек |
| 2 | Количество родившихся | человек |
| 3 | Коэффициент рождаемости | промилле |
| 4 | Количество умерших | человек |
| 5 | Коэффициент смертности | промилле |
| 6 | Количество прибывших | человек |
| 7 | Коэффициент прибытия | промилле |
| 8 | Количество выбывших | человек |
| 9 | Коэффициент выбытия | промилле |
| 10 | Естественный прирост (убыль) | человек |
| 11 | Коэффициент естественного прироста (убыли) | промилле |
| 12 | Миграционный прирост (убыль) | человек |
| 13 | Коэффициент миграционного прироста (убыли) | промилле |
В Модели используются следующие обозначения для параметров и вспомогательных показателей:
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 1 | \(t\) | Время (календарная дата), год (месяц, день, час) | год |
| 2 | \(N\) | Численность населения | человек |
Фактические значения по данным федеральной службы государственной статистики (ФСГС)
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 3 | \(N_{[20ХХ]}\) | Фактическая численность на 1 января 20ХХ года | человек |
| 4 | \(B_{[20ХХ]}\) | Количество родившихся в 20ХХ году | человек в год |
| 5 | \(D_{[20ХХ]}\) | Количество умерших в 20ХХ году | человек в год |
| 6 | \(E_{[20ХХ]} = B_{[20ХХ]} – D_{[20ХХ]}\) | Естественный прирост (убыль) в 20ХХ году | человек в год |
| 7 | \(I_{[20ХХ]}\) | Количество прибывших на ПМЖ в 20ХХ году | человек в год |
| 8 | \(O_{[20ХХ]}\) | Количество убывших на ПМЖ в 20ХХ году | человек в год |
| 9 | \(M_{[20ХХ]} = I_{[20ХХ]} – O_{[20ХХ]}\) | Миграционный прирост (убыль) в 20ХХ году | человек в год |
| 10 | \(∆N_{[20ХХ]} = E_{[20ХХ]} + M_{[20ХХ]}\) | Прирост (убыль) населения в 20ХХ году | человек в год |
| 11 | \(K_{Р[20ХХ]} = 2000·B_{[20ХХ]} / (N_{[20ХХ]} + N_{[20ХХ + 1]})\) | Коэффициент рождаемости, равный количеству родившихся в 20ХХ году на тысячу человек населения в 20ХХ году | промилле/год |
| 12 | \(K_{С[20ХХ]} = 2000·D_{[20ХХ]} / (N_{[20ХХ]} + N_{[20ХХ + 1]})\) | Коэффициент смертности, равный количеству умерших в 20ХХ году на тысячу человек населения в 20ХХ году | промилле/год |
| 13 | \(K_{Е[20ХХ]} = K_{Р[20ХХ]} – K_{С[20ХХ]}\) | Коэффициент естественного прироста (убыли) населения | промилле / год |
| 14 | \(K_{П[20ХХ]} = 2000·I_{[20ХХ]} / (N_{[20ХХ]} + N_{[20ХХ + 1]})\) | Коэффициент миграционного прибытия, равный количеству прибывших на ПМЖ в 20ХХ году на тысячу человек населения в 20ХХ году | промилле / год |
| 15 | \(K_{У[20ХХ]} = 2000·O_{[20ХХ]} / (N_{[20ХХ]} + N_{[20ХХ + 1]})\) | Коэффициент миграционного убытия, равный количеству убывших на ПМЖ в 20ХХ году на тысячу человек населения в 20ХХ году | промилле / год |
| 16 | \(K_{М[20ХХ]} = K_{П[20ХХ]} – K_{У[20ХХ]}\) | Коэффициент миграционного прироста (убыли) населения | промилле / год |
| 17 | \(K_{[20ХХ]} = K_{Е[20ХХ]} + K_{М[20ХХ]}\) | Коэффициент прироста (убыли) населения | промилле / год |
Расчетные
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 18 | \(N(t)\) | Расчетная численность на момент времени t | человек |
| 19 | \(N`(t)=dN/dt\) | Скорость изменения численности | человек в год |
| 20 | \(\nu_{B}(t)\) | Расчетный коэффициент рождаемости в момент времени t | 1 / год |
| 21 | \(\nu_{D}(t)\) | Расчетный коэффициент смертности в момент времени t | 1 / год |
| 22 | \(B_{(20XX)}\) | Расчетное количество родившихся в 20ХХ году | человек в год |
| 23 | \(D_{(20XX)}\) | Расчетное количество умерших в 20ХХ году | человек в год |
| 24 | \(E_{(20XX)} = B_{(20XX)} - D_{(20XX)}\) | Расчетный естественный прирост (убыль) в 20ХХ году | человек в год |
| 25 | \(w_{I}(t)\) | Скорость миграционного прибытия в момент времени t | человек в год |
| 26 | \(w_{O}(t)\) | Скорость миграционного убытия в момент времени t | человек в год |
| 27 | \(I_{(20XX)}\) | Расчетное количество прибывших на ПМЖ в 20ХХ году | человек в год |
| 28 | \(O_{(20XX)}\) | Расчетное количество убывших на ПМЖ в 20ХХ году | человек в год |
| 29 | \(M_{(20XX)} = I_{(20XX)} - O_{(20XX)}\) | Расчетный миграционный прирост (убыль) в 20ХХ году | человек в год |
| 30 | \(∆N_{(20XX)} = E_{(20XX)} + M_{(20XX)}\) | Расчетный прирост (убыль) населения в 20ХХ году | человек в год |
Погрешности аппроксимации
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 31 | \(\varepsilon_{N_{[20XX]}} = N_{(20XX)} - N_{[20XX]}\) | Абсолютная ошибка по численности на 1 января 20ХХ года | человек |
| 32 | \(\varepsilon_{B_{[20XX]}} = B_{(20XX)} - B_{[20XX]}\) | Абсолютная ошибка по количеству родившихся в 20ХХ году | человек |
| 33 | \(\varepsilon_{D_{[20XX]}} = D_{(20XX)} - D_{[20XX]}\) | Абсолютная ошибка по количеству умерших в 20ХХ году | человек |
| 34 | \(\varepsilon_{E_{[20XX]}} = E_{(20XX)} - E_{[20XX]}\) | Абсолютная ошибка по естественному приросту (убыли) в 20ХХ году | человек |
| 35 | \(\varepsilon_{I_{[20XX]}} = I_{(20XX)} - I_{[20XX]}\) | Абсолютная ошибка по количеству прибывших на ПМЖ в 20ХХ году | человек |
| 36 | \(\varepsilon_{O_{[20XX]}} = O_{(20XX)} - O_{[20XX]}\) | Абсолютная ошибка по количеству убывших на ПМЖ в 20ХХ году | человек |
| 37 | \(\varepsilon_{M_{[20XX]}} = M_{(20XX)} - M_{[20XX]}\) | Абсолютная ошибка по миграционному приросту (убыли) в 20ХХ году | человек |
| 38 | \(\varepsilon_{∆N_{[20XX]}} = ∆N_{(20XX)} - ∆N_{[20XX]}\) | Абсолютная ошибка по приросту (убыли) населения в 20ХХ году | человек |
Статистические оценки
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 39 | \(P\) | Доверительная вероятность (для решений, приведенных в разделе 8, вероятность \(P\) принята равной 90 %) | % |
| 40 | \(z_{[P]}\) | Квантиль, соответствующий вероятности \(P\), и зависящий, в соответствии с распределением Стьюдента, от количества параметров, входящих в уравнения для численности \(N(t)\) и количества точек, в которых вычисляются ошибки (решения, приведенные в разделе 8, включают 16 параметров и построены по 90 фактическим статистическим значениям) | число |
| 41 | \(err(t)\) | Относительная ошибка (таблица раздела 8) | % |
Результаты расчетов и прогнозирование
| № | Символ | Наименование | Ед. изм. |
|---|---|---|---|
| 42 | \(N(t),\nu_{B}(t),\nu_{D}(t),B(t),D(t),…\) | Расчетные зависимости численности (коэффициента рождаемости, коэффициента смертности, количества родившихся, количества умерших и т. д.) от времени (фиолетовая кривая на графике в разделе 6) | число |
| 43 | \(H(t)=N(t)e^{(z_{[P]}err(t))}\) | Верхние границы прогнозируемого показателя с доверительной вероятностью \(P\) (красная кривая на графике в разделе 6) | число |
| 44 | \(L(t)=N(t)e^{(-z_{[P]}err(t))}\) | Нижние границы прогнозируемого показателя с доверительной вероятностью \(P\) (зеленая кривая на графике в разделе 6) | число |
7.1.3 Используемые формулы и допущения
В самом общем виде соотношение для изменения численности во времени
\[\begin{align*}
N`(t)=dN/dt,
\end{align*}\]
может быть записано в виде:
\[\begin{align*}
N`(t)=N(t)[\nu_{B}(N(t),t,S(N(t),t),Ext(t),…)-\nu_{D}(N(t),t,…)]+\\
+[w_{I}(N(t),t,S(N(t),t),Ext(t),…)-w_{O}(N(t),t,…)], (1)
\end{align*}\]
где
\(N(t)\) - численность населения в зависимости от времени;
коэффициенты рождаемости \(\nu_{B}(N(t),t,S(N(t),t),Ext(t),…)\) и смертности \(\nu_{D}(…)\), а также скорости миграционного прибытия \(w_{I}(…)\) и убытия \(w_{O}(…)\) зависят, в свою очередь, от численности \(N\), времени \(t\), «структуры» населения \(S\) (половозрастной, образовательной, национальной и т. д.), меняющейся во времени, внешних условий \(Ext\) (природно-климатические, уровень инфляции, курс доллара, стоимость нефти, обеспеченность работой, обеспеченность жильем, эпидемии, стихийные и техногенные катастрофы).
В предлагаемой модели рассматриваются два уровня детализации.
Уровень I – для моделирования и анализа социально-экономического развития в целом. Рассчитывается численность населения с последующим разделением на три возрастные группы:
- моложе трудоспособного возраста,
- трудоспособного возраста,
- старше трудоспособного возраста.
Уравнение (1) сводится к виду (2):
\[\begin{align*}
N`(t)=N(t)[\nu_{B}(t)-\nu_{D}(t)]+[w_{I}(t)-w_{O}(t)], (2)
\end{align*}\]
где функции \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\) включают в себя зависимости от «структуры», в свою очередь, от численности \(N\), времени \(t\), «структуры» населения и внешних условий без детализации.
Основная проблема моделирования заключается в том, что функции \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\) – неизвестны, то есть задача является «обратной», что на порядок повышает сложность решения. Порядок решения приведен в разделе 5 настоящего раздела.
Уровень II - предназначен для детального моделирования и анализа развития демографической системы.
Для уровня II уравнения (3) строятся отдельно для каждой i-ой возрастной группы с добавлением процесса «старения» - перехода из одной возрастной группы
в следующую по возрасту:
\[\begin{align*}
N`_{i}(t)=N_{i}(t)[\nu_{B_{i}}(t)-\nu_{D_{i}}(t)]+[w_{I_{i}}(t)-w_{O_{i}}(t)]+[u_{I_{i}}(t,S)-u_{O_{i}}(t,S)]. (3)
\end{align*}\]
где функции \(u_{I_{(i+1)}}(t,S)=u_{O_{i}}(t,S)\) – функции входа / выхода в i-ю возрастную группу.
Функции \(u_{I_{i}}(t,S)\), \(u_{O_{i}}(t,S)\), в отличие от неизвестных функций \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\), известны и полностью определяются половозрастной структурой \(S\) и временем \(t\).
7.1.4 Исходные данные для модели
Исходными данными для модели Уровня I являются ретроспективные временные ряды по данным ФСГС (для тех лет, где они имеются):
\(N_{[2000]}, N_{[2001]}, …, N_{[2023]}\) - Фактическая численность на 1 января 20ХХ года, человек
\(B_{[2000]}, B_{[2001]}, …, B_{[2022]}\) - Количество родившихся в 20ХХ году, человек / год
\(D_{[2000]}, D_{[2001]}, …, D_{[2022]}\) - Количество умерших в 20ХХ году, человек / год
\(I_{[2000]}, I_{[2001]}, …, I_{[2022]}\) - Количество прибывших на ПМЖ в 20ХХ году, человек / год
\(O_{[2000]}, O_{[2001]}, …, O_{[2022]}\) - Количество убывших на ПМЖ в 20ХХ году, человек / год
7.1.5 Описание итоговых показателей расчета
Итоговые показатели расчета включают в себя следующие параметры для каждого демографического показателя:
Год — номер года характеризующий период, на окончание которого рассчитано значение показателя;
Период, начало — дата, характеризующая начало расчетного периода с точностью до 1 дня, для 2023 года будет равняться 01.01.2023;
Период, окончание — дата, характеризующая окончание расчетного периода с точностью до 1 дня, для 2022 года будет равняться 31.12.2022;
Факт — фактическое (не расчетное) значение демографического показателя на соответствующую дату, берется из паспорта города;
План/Проект — значение прироста (убыли) демографического показателя, вызванного не естественными процессами, а управляемым воздействием (например, присоединением новой области к муниципальному образованию);
Скачок — бинарный параметр, который находится во включенном состоянии (значение — TRUE) если введено значение “План/Проект“, в остальных случаях находится в выключенном состоянии;
Расчет, среднее — показывает наиболее ожидаемое прогнозное значение ряда демографических данных;
Расчет, верхняя граница — ряд характеризует верхнюю границу коридора прогнозируемых значений, в который должны попасть 90% ожидаемых значений;
Расчет, нижняя границы — ряд характеризует верхнюю границу коридора прогнозируемых значений, в который должны попасть 90% ожидаемых значений.
7.1.6 Детальное описание алгоритма произведения расчетов
Шаг 1. Выбор вида функций \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\). Простейшими функциями, имеющими «физический» смысл, то есть пригодными не только для аппроксимации в ретроспективном периоде, но и для экстраполяции на прогнозный период являются четырех-параметрические сигмоидальные кривые [С. П. Капица]. В настоящей работе используется форма (4):
\[\begin{align*}
& \nu_{B}(t)=\frac{a_{B}+b_{B}(t⁄d_{B})^{c_{B}}}{1+(t⁄d_{B})^{c_{B}}}, & (4B) \\
& \nu_{D}(t)=\frac{a_{D}+b_{D}(t⁄d_{D})^{c_{D}}}{1+(t⁄d_{D})^{c_{D}}}, & (4D) \\
& w_{I}(t)=\frac{a_{I}+b_{I}(t⁄d_{I})^{c_{I}}}{1+(t⁄d_{I})^{c_{I}}}, & (4I) \\
& w_{O}(t)=\frac{a_{O}+b_{O}(t⁄d_{O})^{c_{O}}}{1+(t⁄d_{O})^{c_{O}}} & (4O)
\end{align*}\]
где a, b, c, d – параметры соответствующих соотношений;
a – значение функции при t = 0 (за 0 принято 1 января 1999 года);
b – предельный уровень функции при t = \(\infty\) (в «будущем»);
d – дата перегиба функции при t = d;
c – определяет угол наклона кривой в точке перегиба.
Шаг 2. Определение начальных значений параметров. Начальные значения параметров a, b, c, d определяются методом наименьших квадратов независимо для каждой из функций \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\), с использованием соответствующих временных рядов.
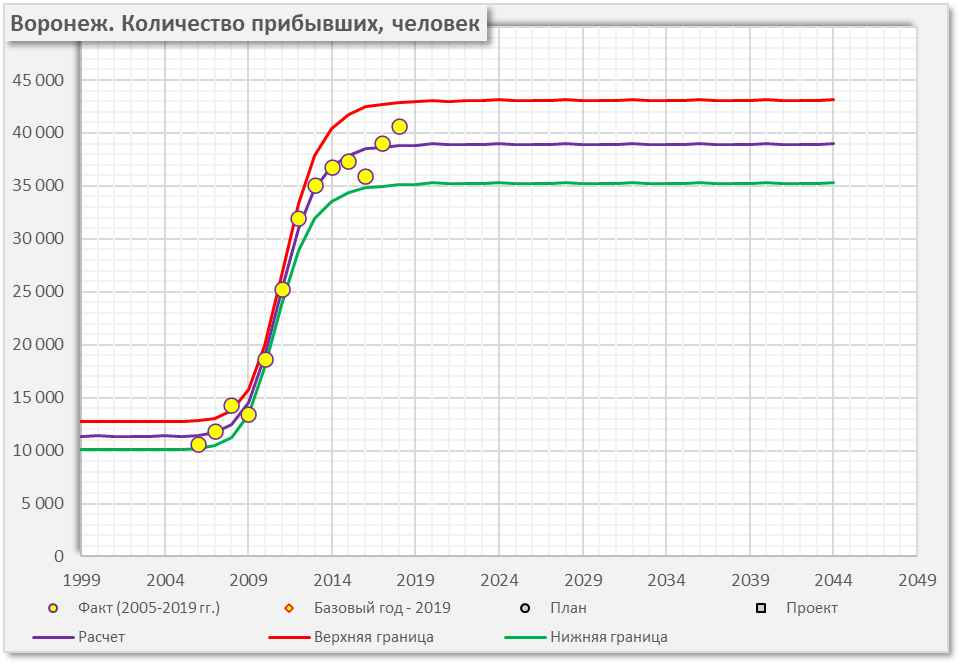На рисунке приведен пример построения сигмоидальной функции \(w_{I}(t)\) для Воронежа.
В приведенном примере a = 11046 человек / год, b = 37894 человек / год, d = 12.71 года, т. е. дата перегиба 14 мая 2011 года, с = 11.8, что показывает резкий переход от одного уровня до другого.
Шаг 3.1. Решение дифференциального уравнения (2) на ретроспективный период.
Для решения уравнения:
\[\begin{align*}
N`(t)=N(t)[\nu_{B}(t)-\nu_{D}(t)]+[w_{I}(t)-w_{O}(t)], (2)
\end{align*}\]
применяется неявный метод Эйлера.
Дифференциальное уравнение (2) заменяется разностным:
\[\begin{align*}
&\frac{N(t_{j}+δt)-N(t_{j})}{δt}=\frac{N(t_{j})\nu_{B}(t_{j})+N(t_{j}+δt)\nu_{B}(t_{j}+δt)}{2}-\frac{N(t_{j})\nu_{D}(t_{j})+N(t_{j}+δt)\nu_{D}(t_{j}+δt)}{2}+\\
&+\frac{w_{I}(t_{j})+w_{I}(t_{j}+δt)}{2}-\frac{w_{O}(t_{j})+w_{O}(t_{j}+δt)}{2}. (5)
\end{align*}\]
Перенося значения \(N(t_{j}+δt)\) в левую часть, получаем
\[\begin{align*}
&N(t_{j}+δt)(1-\frac{\nu_{B}(t_{j}+δt)δt}{2}+\frac{\nu_{D}(t_{j}+δt)δt}{2})=N(t_{j})(1+\frac{\nu_{B}(t_{j})δt}{2}-\frac{\nu_{D}(t_{j})δt}{2})+\\
&+δt(\frac{w_{I}(t_{j})+w_{I}(t_{j}+δt)}{2}-\frac{w_{O}(t_{j})+w_{O}(t_{j}+δt)}{2}). (6)
\end{align*}\]
Из соотношения (6) определяется \(N(t_{j+1})=N(t_{j}+δt)\) для следующего момента времени.
Для решения в ретроспективной области в качестве начального момента времени \(t_{0}\) принимается последняя дата, для которой известно значение численности (в примерах разделов 9 и 10 - 1 января 2019 года), а шаг \(δt\) задается отрицательным (1 месяц).
Шаг 3.2. Параллельно с решением для численности определяются расчетные значения других показателей: количество родившихся, умерших, прибывших на ПМЖ, убывших на ПМЖ.
Шаг 4. Оценка ошибок. Результаты расчетов по шагам 3.1 и 3.2 сравниваются с фактическими значениями и определяются погрешности аппроксимации \(\varepsilon_{N_{[20XX]}} = N_{(20XX)} - N_{[20XX]}\), \(\varepsilon_{B_{[20XX]}} = B_{(20XX)} - B_{[20XX]}\) и т. д. Общей оценкой ошибок считается сумма квадратов погрешностей \(∑\varepsilon^{2}\) по всем фактическим значениям (в примере из разделов 9, 10 фактических значений 90 по 15 показателям).
Шаг 5. Уточнение параметров функций \(\nu_{B}(t)\), \(\nu_{D}(t)\), \(w_{I}(t)\) и \(w_{O}(t)\). Поправки к параметрам a, b, c, d рассчитываются методом Ньютона безусловной оптимизации суммы квадратов погрешностей \(∑\varepsilon^{2}\).
Шаг 6. Итерационное повторение шагов 3, 4, 5 до достижения возможного минимума суммы квадратов погрешностей.
Шаги 7.1 и 7.2 Решение дифференциального уравнения (2) на прогнозный период. Шаги 7.1 и 7.2 полностью аналогичны шагам 3.1 и 3.2 за исключением того, что шаг по времени \(δt\) задается положительным (1 месяц).
Шаг 8. Построение верхней и нижней границ прогноза. Ошибка аппроксимации \(err(t)\) включают две составляющие: постоянную \(\varepsilon_{const}\) и переменную \(\varepsilon_{var}|t-t_{0}|\), равную 0 в начальной точке \(t_{0}\) (в представленных результатах \(t_{0}\) соответствует 1 января 2019 года)
\[\begin{align*}
err(t)^{2}=\varepsilon_{const}^{2}+\varepsilon_{var}^{2}(t-t_{0} ). (7)
\end{align*}\]
Для построения верхней \(H(t)\) и нижней \(L(t)\) границ ошибка \(err(t)\) умножается на квантиль \(z_{[P]}\), зависящий от доверительной вероятности \(P\), количества параметров и количества фактических значений (для приведенного примера при \(P=90\%\), 16-ти параметрах и 90 фактических значений \(z_{[90\%]} = 1.673\)):
\[\begin{align*}
&H(t)=N(t)e^{(z_{[P]}err(t))}, & (8) \\
&L(t)=N(t)e^{(-z_{[P]}err(t))}. & (9)
\end{align*}\]
7.1.7 Область (границы) допустимого применения математической модели
Данная модель подходит для прогнозирования населения города при его естественном и постепенном развитии, и не может показывать высокую точность и предсказывать, когда на демографические показатели города воздействуют резкие и значительные внешние изменения (войны, природные и техногенные катастрофы), а также в случае изменения границ населенного пункта или методики подсчета населения — что дает резкие «рукотворные» скачки значений демографических.
При этом, Модель позволяет провести сценарный анализ или прогноз, в случае если на вход Модели подставить «рукотворное» изменение показателей.
В случае объединения двух населенных пунктов в период, за который берутся данные для прогнозной модели необходимо провести расчет для каждого населенного пункта раздельно, а потом арифметически сложить получившиеся значения.
Также, расчеты подходят только для прогнозирования годовых значений и не сглаживают демографические волны и иные волнообразные эффекты для которых будет разработана отдельная модель системной динамики, учитывающая тренды полученные по результатам расчетов данной Модели.
7.1.8 Оценка точности математических моделей
Оценка по ретроспективным данным показывает высокую точность расчета численности населения (до 0,18 %) и средних значений частных показателей. В то же время сузить коридор между нижней и верхней границей не представляется возможным, так как некоторые точки лежат на границах коридора или даже выходят за них. При доверительной вероятности 90 % из 90 точек 8-10 должны «выпадать» из коридора. Оценивая точность прогноза с фактическими данными на 1 января 2020 года погрешность для 4 из 5 городов не превышает 1% от населения города (для Архангельска – 118 человек, Воронежа – 398 человек, Краснодара – 7227 человек, Уфы – 57 человек, Южно-Сахалинска – 2272 человек). При этом для трех городов прогноз показывает особенно высокую точность — отклонение менее 0,05%.
Численность населения, человек
| Город | Прогноз на 2020* | Факт | Отклонение |
|---|---|---|---|
| Воронеж | 1 057 863 | 1 058 261 | -0,04% |
| Краснодар | 939 856 | 932 629 | 0,77% |
| Уфа | 1 128 730 | 1 128 787 | -0,01% |
| Архангельск | 346 861 | 346 979 | -0,03% |
| Южно-Сахалинск | 202 908 | 200 636 | 1,13% |
* прогноз создан на основе данных за 2000—2019 года
Таблица иллюстрирует точность текущих расчетов по сравнению с новыми фактическими данными о населении пяти городов.
